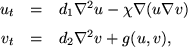The model for chemotaxis proposed by Keller and Segel [6] serves as a paradigm for the oriented movement (or taxis) of a cell concentration
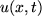 in response to a chemical concentration
in response to a chemical concentration 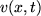 that is in turn produced by the cells. The model is given by:
that is in turn produced by the cells. The model is given by:
where
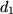 and
and 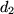 are diffusion constants for
are diffusion constants for  and
and  respectively,
respectively, 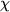 is the chemotactic parameter responsible for the cross diffusion
term and the function
is the chemotactic parameter responsible for the cross diffusion
term and the function 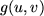 accounts for the reaction terms. The net effect of the taxis
is that the cells aggregate to form spikes. In collaboration with the mathematical
biology group at University of British Columbia led by Leah Keshet, we are
studying formation of patterns and their stability as models for the formation
of malign plaques in the brain for Alzheimer's disease. We employ ad-hoc moving
mesh techniques for the accurate computation of solutions.
accounts for the reaction terms. The net effect of the taxis
is that the cells aggregate to form spikes. In collaboration with the mathematical
biology group at University of British Columbia led by Leah Keshet, we are
studying formation of patterns and their stability as models for the formation
of malign plaques in the brain for Alzheimer's disease. We employ ad-hoc moving
mesh techniques for the accurate computation of solutions.
In one spatial dimension, chemotactic models possess spike solutions whose height saturates with time. I am currently studying spike-spike and spike-boundary interactions in collaboration with Bob Russell and Michael Ward (University of British Columbia). These interactions yield interesting dynamics including exponentially small spike movement (metastability). We are currently studying the mechanisms responsible for metastability where traditional techniques (matching asymptotic analysis) fail [7]. We also employ ad-hoc moving mesh methods to validate our findings. Without the use of specialized moving mesh techniques one fails to accurately describe the spike evolution (artificial spatial pinning of the spikes and creation of spikes at the wrong locations). We are also interested in the possibility of finding non-trivial steady multi-spike solutions [8].
In dimensions higher than one, chemotactic models (and other reaction diffusion equations) are prone to blow-up of the solutions in finite time [9]. For these kind of models, even adaptive mesh methods often fail to accurately follow blow-up solutions for long times and one has to be careful on adopting the appropriate adaptive technique [10]. I am currently investigating the possibility of using the self-similarity (or near self-similarity) properties of the blowing solutions for their accurate computation.
The implementation of reliable moving mesh techniques in dimensions higher than one is a cumbersome task. Current techniques fail to follow the blowing-up region due to a saturation of the mesh concentration near the blow-up. In collaboration with Weiming Cao at UTSA, Texas, we are currently investigating the effects of spatio-temporal mesh smoothing and self similarity for blow-up solution in two dimensions. We believe that these effects are responsible for the saturation of mesh movement that leads to failure of the numerics.