



Next: Reaction-diffusion and cross-diffusion
Up: Spatially extended systems
Previous: Spatially extended systems
Contents
The Nonlinear Shrödinger equation (NLS):
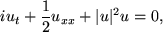 |
(1) |
accepts exact multi-soliton solutions [1]. However, these formulae quickly become
prohibitive even for a handful of interacting solitons. Thus an alternative approach
is needed in order to follow the interaction of large numbers of solitons. The
idea is to approximate every soliton of the multi-soliton solution by a one-soliton
solution: ![$
u_k(x,t)= \nu_k(t) {\rm sech}(\nu_k(t)(x -\xi_k(t)))
e^{i[\mu_k(t)(x -\xi_k(t))+\delta_k(t)]},
$](gifs/img2.gif.crop.gif) with time dependent parameters: position
with time dependent parameters: position 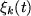 , width
, width 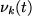 , velocity
, velocity 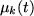 and phase
and phase 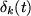 . With this ansatz it is possible to apply perturbation techniques
[2] and/or variational methods [3] to determine the evolution of the soliton
parameters. The originally infinite-dimensional system (a PDE) is then reduced
to a lattice of coupled ODEs, or lattice differential equation (LDE), on the soliton
parameters:
. With this ansatz it is possible to apply perturbation techniques
[2] and/or variational methods [3] to determine the evolution of the soliton
parameters. The originally infinite-dimensional system (a PDE) is then reduced
to a lattice of coupled ODEs, or lattice differential equation (LDE), on the soliton
parameters:
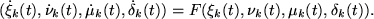 |
(2) |
Using this reduction it is possible to apply
dynamical systems ideas to study the possible interactions
in the soliton chain.
- Applications to fiber optics communication:
Hyper-solitons [t.4]
Using the LDE reduction it is possible to obtain novel soliton dynamics
describing the propagation of a compressive wave in the soliton positions
through the lattice. This compressive wave corresponds to a
soliton of the LDE that in turn translates as a soliton of
solitons, a Hyper-soliton, of the original PDE (1).
- Applications to Bose-Einstein condensates:
Localized Breathers [s.2,t.4,w.4]
By adding a periodic potential 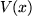 to the NLS
to the NLS
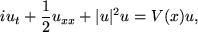 |
(3) |
one may describe the behaviour of interacting aggregate of coherent matter --Bose-Einstein
Condensates (BECs) [4]-- under certain physical conditions. After
reducing the governing PDE we obtain a new LDE that describes the interactions
between neighboring BECs pinned on a regular lattice. We show how the inclusion
of the periodic potential allows for the existence of time-periodic, exponentially
localized vibrations: breathers. We assume the parameters of each soliton
oscillating with a common frequency 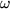 but different amplitudes
but different amplitudes 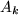 . We further reduce the dynamics and find a two-dimensional map relating
. We further reduce the dynamics and find a two-dimensional map relating
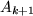 to
to 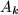 and
and 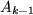 . The exponentially localized vibration correspond to homoclinic
connections or tangles of the stable and unstable manifolds of the origin
[5].
. The exponentially localized vibration correspond to homoclinic
connections or tangles of the stable and unstable manifolds of the origin
[5].
- Future directions:
Extended vibrational solutions of the BECs and their stability [w.4]
Using the above approach and looking for more general kinds
of connections or tangles (homoclinic or heteroclinic) emanating
from points away from the origin, it should be possible to obtain
extended (i.e. no longer localized) vibrational modes of the
soliton parameters. This technique would allow us to construct
a much richer plethora of solutions.
In the same spirit, I would like to investigate the possibility of
deducing the stability of the above solutions using the
dynamical reduction approach.




Next: Reaction-diffusion and cross-diffusion
Up: Spatially extended systems
Previous: Spatially extended systems
Contents
Ricardo Carretero
2002-08-02
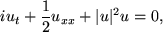




![$
u_k(x,t)= \nu_k(t) {\rm sech}(\nu_k(t)(x -\xi_k(t)))
e^{i[\mu_k(t)(x -\xi_k(t))+\delta_k(t)]},
$](gifs/img2.gif.crop.gif) with time dependent parameters: position
with time dependent parameters: position 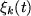 , width
, width 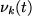 , velocity
, velocity 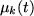 and phase
and phase 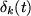 . With this ansatz it is possible to apply perturbation techniques
[2] and/or variational methods [3] to determine the evolution of the soliton
parameters. The originally infinite-dimensional system (a PDE) is then reduced
to a lattice of coupled ODEs, or lattice differential equation (LDE), on the soliton
parameters:
. With this ansatz it is possible to apply perturbation techniques
[2] and/or variational methods [3] to determine the evolution of the soliton
parameters. The originally infinite-dimensional system (a PDE) is then reduced
to a lattice of coupled ODEs, or lattice differential equation (LDE), on the soliton
parameters: 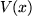 to the NLS
to the NLS 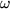 but different amplitudes
but different amplitudes 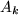 . We further reduce the dynamics and find a two-dimensional map relating
. We further reduce the dynamics and find a two-dimensional map relating
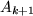 to
to 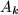 and
and 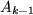 . The exponentially localized vibration correspond to homoclinic
connections or tangles of the stable and unstable manifolds of the origin
[5].
. The exponentially localized vibration correspond to homoclinic
connections or tangles of the stable and unstable manifolds of the origin
[5].



