This session will examine several graphics routines with vector Calculus, then show how Maple can be applied to differential equations. Data is fit to a cubic polynomial, then graphed. 3-D surfaces are plotted, then the volume and surface integrals are analyzed. The Divergence and Stokes' Theorems are visualized, then special functions, including gradient and curl are applied. We include the LaTeX command to show how to generate latex code for good document presentation. The graphics ends with animations of Fourier series and a parametrized 3-D surface. Several techniques for solving differential equations are shown, including exact solutions, series solutions, and numerical techniques. The differential equations are visualized using several graphics packages, including direction fields and phaseportraits. As usual, there is a hyperlink to the Maple Worksheet for this lecture.

Graphics

Maple's graphics capabilities cover a variety areas using several special packages. These require special tools and some are shown below.

Fitting Data

Suppose we want to fit data to a cubic model and visualize both the data and the model. Our example comes from the oxygen consumption of the "kissing bug," Triatoma phyllosoma , during the fourth instar stage (Data from Boyd Collier). This bug carries chagas disease. The time data (in hours) is stored as td, while the oxygen consumption is stored as yd.

> td := [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]: yd := [116.6, 120.1, 114.9, 129.9, 116.5, 107.7, 99.0, 104.0, 100.7, 87.5, 82.7, 53.8, 54.0, 72.4, 81.1]:

We will use the statistics package (for least squares), the statistics plotting package (for scatterplot), and the plotting package (for displaying two types of graphs).

> with(stats): with(stats[statplots]): with(plots):

Graph the data with circles for points, then store this graph for later. First view the graph, then store the picture.

> plots[display](scatterplot(td,yd),symbol=circle);

> Data := plots[display](scatterplot(td,yd),symbol=circle):

Create a general cubic model.

> model := a*t^3 + b*t^2 + c*t + d;

Find the least squares best fit of the cubic model to the data.

> eqn := fit[leastsquare[[t,y], y=model, {a,b,c,d}]]([td, yd]);

Make y into a function depending on t .

> y := unapply(rhs(eqn),t);

Store the graph of the model, then display it with the graph of the data.

> Y := plot(y(t),t=0..15):

> display({Data,Y});

Select individual coefficients from the model.

> b := coeff(y(t),t,2);

Volume and Surface Area

Maple provides a good tool for visualizing the 3-D surfaces from vector Calculus. It can be readily used to find the surface area and volume of these 3-D objects. Consider the following paraboloid.

To visualize this surface in Maple, we need to parameterize the x , y , and z components into 2 parameters. I want the graph centered on the origin (axes = NORMAL) and the picture unscaled (scaling = CONSTRAINED).

> r := [u*cos(v)/2,u*sin(v),4-u^2];

> plot3d([r[1],r[2],r[3]],u=0..2,v=0..2*Pi,axes = NORMAL, labels = [x,y,z], scaling = CONSTRAINED, orientation = [40,70]);

We find the volume under this surface (using symmetry).

> 4*Int(Int(4-4*x^2-y^2,y=0..sqrt(4-4*x^2)),x=0..1);

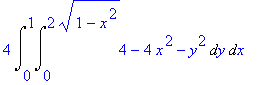
The formula can be inserted into a LaTeX document by letting Maple generate the code.

> latex(%);

4\,\int _{0}^{1}\!\int _{0}^{2\,\sqrt {1-{x}^{2}}}\!4-4\,{x}^{2}-{y}^{

2}{dy}\,{dx}

Below we compute the double integral.

> 4*int(int(4-4*x^2-y^2,y=0..sqrt(4-4*x^2)),x=0..1);

We find the surface area of this surface (again using symmetry). A reminder that if z = f ( x , y ), then the formula for computing the area of the surface is

 

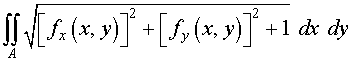
> f := (x,y) -> 4 - 4*x^2 - y^2;

> 4*Int(Int(sqrt((diff(f(x,y),x))^2+(diff(f(x,y),y))^2+1),y=0..sqrt(4-4*x^2)),x=0..1);

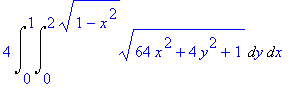
> 4*int(int(sqrt((diff(f(x,y),x))^2+(diff(f(x,y),y))^2+1),y=0..sqrt(4-4*x^2)),x=0..1);

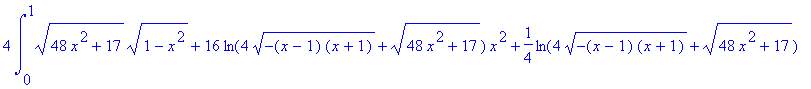
> evalf(%);

An alternate method for computing surface integrals uses the following formula

 

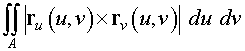
> with(linalg):

We created the parametrized surface by the function r ( u , v ) given above. By taking the crossproduct of the partial derivatives of the parametrized surface function, we obtain the outward normal to the surface.

> ruxrv := crossprod(diff(r,u),diff(r,v));

> absruxrv := sqrt(ruxrv[1]^2 + ruxrv[2]^2 + ruxrv[3]^2);

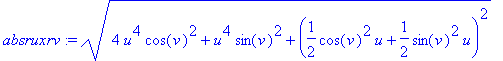
The area of the surface is the integral over the range of the parameters of the magnitude of the outward normal. One could use the norm function, but Maple has difficulty integrating quantities with absolute values.

> int(int(absruxrv, u = 0..2),v = 0..2*Pi);

Often when the integral cannot be evaluated exactly, the evalf function allows numerical solution of the integral.

> evalf(%);

Gauss' and Stokes' Theorems

Two of the major theorems used for fluid flow are the Divergence or Gauss' Theorem and Stokes' Theorem. The Divergence Theorem provides an means of determining the flow through a bounded region in 3-space. Stokes' Theorem gives information on the rotation of a fluid.

Let us consider these theorems for a fluid flowing through a hemisphere. We begin by visualizing the fluid flow and the hemisphere.

> with(plots):

View the fluid flow, using Maple's fieldplot.

> F := [x^2*y, y*z, 2*z-1];

> fieldplot3d(F,x=-4..4,y=-4..4,z=-1..4,grid=[8,8,5],axes = NORMAL, thickness = 2);
Flow := fieldplot3d(F,x=-4..4,y=-4..4,z=-1..4,grid=[8,8,5],axes = NORMAL, thickness = 2):

Graph the hemisphere, which is the surface bounding the region for applying the Divergence and Stokes' Theorem.

> r := [3*cos(u)*cos(v),3*sin(u)*cos(v),3*sin(v)];

> plot3d([r[1],r[2],r[3]],u=0..2*Pi,v=0..Pi/2,axes = NORMAL, labels = [x,y,z], orientation = [40,70], style = WIREFRAME, color = BLACK);
Hemi := plot3d([r[1],r[2],r[3]],u=0..2*Pi,v=0..Pi/2,axes = NORMAL, labels = [x,y,z], scaling = CONSTRAINED, orientation = [40,70], style = WIREFRAME, color = BLACK):

> display3d({Flow,Hemi});

The Divergence Theorem is given by

 

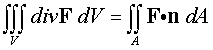
> with(linalg):

Here we compute the divergence of the vector flow field, then integrate this quantity over the volume.

> divF := diverge(F,[x,y,z]);

> Int(Int(Int(divF,z = 0..sqrt(9-x^2-y^2)),y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);

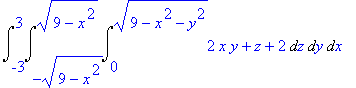
> int(int(int(divF,z = 0..sqrt(9-x^2-y^2)),y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);

> evalf(%);

The above integral is more easily written in spherical coordinates and given by

> Int(Int(Int((2*rho^2*cos(theta)*sin(theta)*sin(phi)^2 + rho*cos(phi) + 2)*rho^2*sin(phi),rho = 0..3),theta = 0..2*Pi),phi = 0..Pi/2);

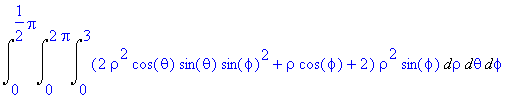
> int(int(int((2*rho^2*cos(theta)*sin(theta)*sin(phi)^2 + rho*cos(phi) + 2)*rho^2*sin(phi),rho = 0..3),theta = 0..2*Pi),phi = 0..Pi/2);

> evalf(%);

Stokes' Theorem measures the circulation around any curve C . If we consider the curve where the hemisphere intersects the xy -plane with the flow F given above, then Stokes' Theorem states that

 

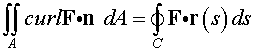
Here we compute the curl of the vector field, then evaluate the double integral over the circle in the xy -plane beneath the hemisphere.

> curlF := curl(F,[x,y,z]);

> curlFn := dotprod(curlF,[0,0,1]);

> Int(Int(curlFn,y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);

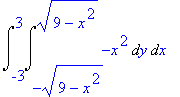
> int(int(curlFn,y = -sqrt(9-x^2)..sqrt(9-x^2)),x = -3..3);

In polar coordinates...

> int(int(-R^3*cos(theta)^2,R = 0..3),theta = 0..2*Pi);

 

Animations

Maple has programs that allow visualization of 2 and 3-D graphics through animations.

We begin with a repeat of our Fourier series expansion from the previous session. However, this time, the evolution of the partial sums of the Fourier series is viewed through animation, which allows one to easily see how the Fourier series is converging. The animation program requires the plots package.

> with(plots):

> bi := int(x*sin(i*Pi*x),x=-1..1);

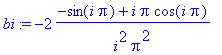
> S := n -> sum(bi*sin(i*Pi*x), i = 1..n);

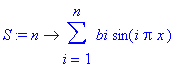
> animate(S(n), x=-3..3,n=1..20,frames=20,numpoints=500, color = blue);

After invoking the animation, a series of buttons appears on the menu bar. These allow the user to view the movie of the graph evolving either forward or backward, cycle through, or go frame by frame.

Below we simply took one of the 3-D examples from Maple's Help. In the 3-D case, the default uses just 8 frames.

> animate3d(cos(t*x)*sin(t*y),x=-Pi..Pi, y=-Pi..Pi,t=1..2,color=cos(x*y));

>

Differential Equations

Maple has tools for solving differential equations and graphing the solutions.

> restart:

The command above clears the variables from the previous section.

Solving Differential Equations

Maple uses a number techniques for solving differential equations, including exact methods, series techniques, and numerical solutions.

> dsolve({diff(y(t),t$2) + 4*diff(y(t),t) + 5*y(t) = 15*t^3, y(0) = 5, D(y)(0) = -2}, y(t));

The equation below is Bessel's equation of second order, which has well known solutions known as Bessel's functions. We use Maple to show the series solution of this equation.

> dsolve(t^2*diff(y(t),t$2) + t*diff(y(t),t) + (t^2-4)*y(t) = 0, y(t));

> dsolve(t^2*diff(y(t),t$2) + t*diff(y(t),t) + (t^2-4)*y(t) = 0, y(t), series);

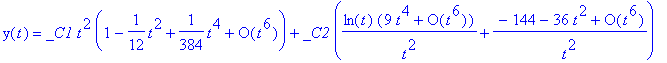
We can increase the number of terms generated by the series solution.

> Order := 12:

> dsolve(t^2*diff(y(t),t$2) + t*diff(y(t),t) + (t^2-4)*y(t) = 0, y(t), series);

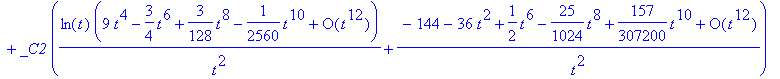
Maple can solve some systems of differential equations.

> sys := {diff(x(t),t) = 2*x(t) - y(t) - 2*z(t), diff(y(t),t) = x(t) + 2*y(t), diff(z(t),t) = 2*x(t) - z(t)};

> dsolve(sys, {x(t),y(t),z(t)});

Many differential equations cannot be solved exactly, but there are numerical methods to solve differential equations. The default method for Maple is the Runge-Kutta Fehlberg 45 method. We use the Lotka-Volterra model to demonstrate the numerical solver.

> ff := dsolve({diff(x(t),t) = x(t)*(1-y(t)), diff(y(t),t) = 0.3*y(t)*(x(t)-1), x(0)=0.2, y(0)=1},
{x(t),y(t)}, type=numeric, output=listprocedure);

> fx := subs(ff,x(t)): fy := subs(ff,y(t)):

Next we use numerical solution to generate a series of points, which are then graphed.

> LVsoln := [seq([fx(0.1*n),fy(0.1*n)], n = 0..200)]:

> plot(LVsoln, title=`Lotka-Volterra Model`, labels=[`prey`,`predator`], color=blue, thickness=2);

Graphic Studies of Differential Equations

Maple has a number of methods for visualizing the solutions of differential equations.

> with(DEtools):

The DEplot routine shows the vector field along with some trajectories of the Lotka-Volterra model. This is a phaseportrait of this predator-prey model.

> DEplot([diff(x(t),t) = x(t)*(1-y(t)), diff(y(t),t) = 0.3*y(t)*(x(t)-1)], [x(t),y(t)], t=0..15, [[x(0)=1.2,y(0)=1.2],[x(0)=1,y(0)=.7]], stepsize=.2,
title=`Lotka-Volterra model`, color = [.3*y(t)*(x(t)-1),x(t)*(1-y(t)),.1],
linecolor=t/2, arrows=MEDIUM, method=rkf45);

Maple has a phaseportrait command. Below we show a 2-D projection of a 3-D plot from the system of equations solved above, using 2 initial conditions.

> phaseportrait([diff(x(t),t) = 2*x(t) - y(t) - 2*z(t), diff(y(t),t) = x(t) + 2*y(t), diff(z(t),t) = 2*x(t) - z(t)], [x(t),y(t),z(t)], t=0..5, [[x(0)=0.1,y(0)=0,z(0)=0], [x(0)=-0.1,y(0)=0,z(0)=0]], stepsize=.05, scene=[x(t),y(t)], linecolour=sin(t*Pi/2));

Maple also produces 3-D plots of differential equations. Below we show the command that produces the graph show on the opening page of this website.

> DEplot3d({D(x)(t)=y(t), D(y)(t)=-x(t)-0.4*y(t)}, [x(t),y(t)], t=0..10, [[x(0)=0,y(0)=1], [x(0)=0,y(0)=.5], [x(0)=0,y(0)=-1], [x(0)=0,y(0)=-.5], [x(0)=1,y(0)=0], [x(0)=0.5,y(0)=0], [x(0)=-1,y(0)=0], [x(0)=-0.5,y(0)=0]], scene=[t,x(t),y(t)], stepsize=.1, title=`Damped Oscillations`, linecolour = t-sqrt(t), axes=NORMAL);