This lab begins by geometrically examining the relationship of the derivative to the slope of a tangent line, then uses the definition of the derivative to find the derivative of a couple of functions. The second part of this question has you use Maple to find the derivative. The second question in this lab fits data to the height of a ball thrown vertically, then uses that information to study the flight of the ball (height and velocity). This is a classic example relating height to its derivative, velocity. The last example starts with a basic model for the length of a species of fish as a function of age, then uses this information to study the derivative of the length, which gives growth rates for the fish as it ages.

Question 1: The first part of this question has you find two points on the curve generated by your function f(x) with the difference in the x values getting closer together. Create a table in Excel with Column A containing the values of x on the interval specified in your lab and separated by 0.05. (That is take the initial value of the interval and put it in cell A1, then let cell A2 have " = A1 + 0.05" in it and fill down to the final value in your interval.) This partitions your curve into enough points to get a smooth curve. In Column B, you enter your function. Compute the slopes of your different lines, then find the equations for each of your lines. Put your lines in Columns C-F, then graph all the values in Columns A-F to get the desired curves.

Computing the slope of the tangent line can be a tedious computation with lots of algebra. Maple does algebra and differentiation extremely well, so the next part of this lab problem uses Maple's symbolic algebra ability to handle the tedious computations. In class, we are finding the slope of the tangent line at a point (x₀, f(x₀)) by looking at the secant line through the points (x₀, f(x₀)) and (x₀ + h , f(x₀ + h)), then letting h tend to zero.

Below is an example that we will go through in lab to help you see the Maple commands for Parts b and c of Problem 1. As an example, let us consider the function

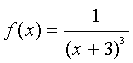
Suppose we want to find the slope of the secant line through the points (-2, f(-2)) = (-2, 1) and (-2 +h, f(-2 +h)) = (-2+h, 1/(1+h)³). (Note that you will be using a value different from x₀= -2, so make the appropriate changes below.) Below is the sequence of Maple commands to find the slope of both the secant and tangent lines.

First, you enter the function in the standard way for Maple:

> f : = x -> 1/(x+3)^3;

The slope of the secant line is found by the following:

> (f(-2+h) - f(-2))/h;
simplify(%);

The simplify command lets Maple find the easiest form of the expression that it chooses. (This may or may not be the best form to analyze.) Next we want the slope of the tangent line, which is found by letting h tend to zero. This is the derivative of f(x) at x = -2.

> m := limit(%, h = 0);

The m := is simply used to define the slope for future use. Maple has the limit command to take limits, which is mathematically a very difficult process. The % in Maple means to take the previous expression and place in the position with the %. (This can be a dangerous command to use, as it works on whatever you just did, not necessarily from the line above. If you do anything else, then use the cursor to return to a line with the %, then you may get the wrong result.)

Next we define tangent line (the command tline(x); gives you the equation of the tangent line), then plot both the function and the tangent line. (You will need to adjust the x and y values in the plot command to get the desired graph for your problem.)

> tline := x -> m*(x - (-2)) + f(-2); tline(x);

> plot({f(x), tline(x)}, x = -3..1, y = -10..20);

This completes Maple needed for the first parts of the problem.

The last part of the problem shows you how easily you can get a derivative using Maple. This is the way that many mathematicians actually do research when they need to accurately differentiate complicated expressions. Biologists often learn about a process through experimentation and recognizing patterns. Maple provides a powerful tool for performing differentiation, so it can act as your experimental device. Let Maple do the differentiations for you, then see if you can recognize patterns that eventually will become rules of differentiation.

You enter your function, for example:

> f := x -> x^2*exp(-1/x);

To differentiate, you simply type

> diff(f(x),x);

This is all that you have to do. Now that you have learned this basic Maple, you can use it to help you with answers to your differentiations in Homeworks. 

Question 2: You start this problem by plotting the time and distance data. Excel's trendline is applied using the polynomial fit with order 2. It is very important that in the options section besides having Excel put the equation on the chart you check the option Set intercept = 0. This gives you the best quadratic fit that you will be using for the height, h(t), that is used in the rest of the problem. Since this is a quadratic equation, you should be able to answer the questions easily about maximum height and when it hits the ground.

The remainder of the problem has you computing average velocities and building your intuition about the derivative. There are a fair number of calculations, so you may want to take advantage of doing many of these calculations on the Excel spreadsheet, which with the pull down option, can rapidly give you many of the necessary answers.

Question 3: This problem starts with the use of Solver to find the nonlinear least squares best fit to the data on the length of a species of fish as it ages. The remainder of this problem has you computing growth rates either directly from the data or from the best fitting function. Again you will be performing a fair number of repetitive computations, so it is advised that you use Excel's pull down feature to accelerate your calculations. This problem should help you build your intuition on how length is related to its derivative, the growth rate.